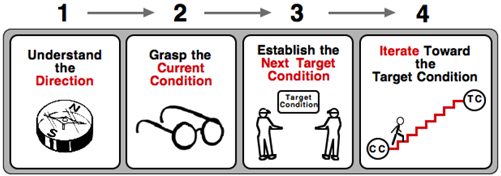
I was going through some old files and came across a pocket card we handed out back in 2003 or so. It was used in conjunction with our “how to walk the gemba” coaching sessions that we did with the lean staff, and then taught them to do with leaders.
There is a pretty long backstory, some of it is summarized in Earl’s recollection on this old post: Genchi Genbutsu in a Warehouse as well as here: The Chalk Circle – Continued.

A lot has happened, a lot has been learned since then. Toyota Kata has been published, and that alone has focused my technique considerably (to say the least).
Nevertheless, I think the elements on these little cards are valuable things to keep in mind.
With that being said, a caveat: Lists like this run the risk of becoming dogma. They aren’t. There are lots of lists like this out there, and the vast majority are very good. The key here is something that a leader or team member can refer to as a reminder that may bias a decision in the right direction. It is the direction that matters, not the reminders.
Fundamentals
The fundamentals are based on the “Rules-in-Use” from Decoding the DNA of the Toyota Production System, a landmark HBR article by Steve Spear and H. Kent Bowen. The article, in turn, summarizes (and slightly updates) Spear’s findings from his PhD work studying Toyota.
A. All work highly specified as to content, sequence, timing, and outcome.
B. Every customer-supplier connection is simple and direct.
C. The path for every product is simple and direct.
D. All improvements are made using PDCA process.
What we left off, though, is that in each of those rules there is a second one: That all of these systems are set up to be “self diagnostic” – meaning there are clear indications that immediately alert the front line people if:
- The work deviates from what was specified.
- The connection between a customer and supplying process is anything other than specified.
- The path a product follows deviates from the route specified.
- Improvements are made outside of a rigorous PDCA (experimental) process.
In other words, the purpose of the rules is to be able to see when we break them, or cannot follow them, so we trigger action.
To put this into Toyota Kata-speak – every process is set up as a target condition that is being run as an experiment – even the process of improvement itself!
Every time there is a disruption – something that keeps the process from running the way it is supposed to – we have discovered an obstacle. That obstacle must first be contained to protect the team members and community (safety) and to protect the customer (quality). Then goes into the obstacle parking lot, and addressed in turn.
If you think about it, the Improvement Kata simply gives us much more rigor to (D).
This ties to the next sections.
Key Leadership Behaviors
Note that this is behaviors. These are things we want leaders to actually strive to do themselves, not just “support.” It was the job of the continuous improvement people to nudge, coach, assist the leaders to move in these directions. It was our job to teach our continuous improvement people how to do that coaching and assisting – beyond just running kaizen events that implement tools.
A. PDCA Thinking
Today we would use Toyota Kata to teach this. But the same structure drove our questioning back then.
B. Four Rules:
1. Safety First
Even though this should be obvious, it is much more common that people are tacitly, or even directly, asked to overlook safety issues for the sake of production. I remember walking through a facility with a group of managers on the way to the area we were going to see. Paul stopped dead in his tracks in front of a puddle on the floor. He was demonstrating just how easy it was for the leadership to walk right past things that should be attended to. And in doing so, they were sending the message – loud and clear in their silence – that having a puddle on the floor was OK.
2. Make a Rule, Keep a Rule
This is a more general instance of Rule #1. But the it is more subtle than it may seem on the surface. Most people immediately interpret this as enforcing organizational discipline, but in reality it is about managerial discipline.
Nearly every organization has a gap between “the rules” and how things really are day-to-day. Sometimes that gap is small. Sometimes it is huge.
Often “rules” are enforced arbitrarily, such as only cases where a violation led to a bigger problem of some kind. Here’s an example: Say your plant has a set of rules about how fork trucks are to be operated – speed limits, staying out of marked pedestrian lanes, etc. But in general the operators hurry, cut a corner now and then. And these violations are typically overlooked… until there is some kind of incident. Then the operator gets written up for “breaking the rules” that everyone breaks every day – and management tacitly encourages people to break every day by focusing on results rather than process.
When we say “make a rule / keep a rule” what we mean is if you aren’t willing to insist on a rule being followed consistently, then take the rule off the books. And if you are uncomfortable taking the rule off the books, then your only option is to develop something that you can stand behind. It might be simple mistake proofing, like physical barriers between forklift aisles and pedestrian aisles. But if you are going to make the rule, then find a way to keep the rule.
Do you have “standard work” documents that are rarely followed? Stop pretending you have standards or rules about how the work is done. Throw them away if you aren’t willing to train to them, mistake proof to them and reinforce following them.
3. Simple is Best
Simply, bias heavily toward the simplest solution that works. The fewest, simplest procedures. The simplest process flow. Complexity hides problems. “Telling people” by the way, is usually less simple than a physical change to the work environment that guides behavior. See above.
4. Small Steps
Again, Toyota Kata’s teaching covers this pretty well today. The key is that by taking small steps, verifying that they work, and anchoring them into practice before taking the next ensures that each step we take has a stable foundation under it.
The alternative would be to make many changes at once in the name of going faster.
We emphasized here that “small steps” does not equal “slow steps.” It is possible to take small steps quickly, and we found that in general doing so was faster than making big leaps. Getting big changes dialed in often required backing out and implementing one thing at a time anyway – just to troubleshoot! See “Gall’s Law” which states:
A complex system that works is invariably found to have evolved from a simple system that worked. A complex system designed from scratch never works and cannot be made to work. You have to start over, beginning with a working simple system.
John Gall, author of Systematics
and sums this up nicely.
C. Ask “Why, what, where, when, who, and how” in that order.
Here we borrowed the sequence from TWI Job Methods. The first two questions challenge whether a process step is even necessary: Why is it necessary? What is its purpose? To paraphrase Elon Musk, the greatest waste of time is improving something that shouldn’t even exist.
Then: Where is the best place? and When is the best time? These questions might nudge thinking about combining steps and further simplifying the process.
And finally we can ask Who is the best person? and “How” is the best method? The key point here is until we have the minimum possible steps in the simplest possible sequence, and understand the cycle times, it doesn’t make sense balance the work cycle or work on improving things.
Come to think about it – perhaps we should ask “How?” before we ask “Who” since improving the method will change the cycle times and may well inform out decisions about the work balance. Hmmm… I’ll have to think about that. Any thoughts from the TWI gurus?
D. Ask Why 5 Times
Honestly, this was a legacy of the times. Unfortunately it suggests that you can arrive at a root cause simply by repeatedly asking “Why?” and writing down the excuses answers that are generated. In reality problem solving involves multiple possible causes at each level, and each must be investigated. I talked about this in a post way back in 2008: Not Just Asking Why – Five Investigations.
E. Go and see.
Go and see for yourself. Taking this into today’s practice, I think it is something that the Toyota Kata community might emphasize a little more. We tend to ask the question “When can we go and see what we have learned…?” but all too often the answer to “What have you learned?” is a discussion at the board rather than actually going and observing. Hopefully the board is close to where the improvement work is being done. Key point for coaches: If the learner can’t show you and explain until you understand, it is likely the learner’s understanding could be deeper.
As You Walk The Workplace:
Check:
perhaps we should have said “Ask…” rather than “Check” but asking and observing are ways to “check.” All of the below are things that the leader walking the workplace must verify by testing the knowledge of the people doing the work.
A. How should the work be done? Content, Sequence, Timing, Outcome
This is another nod to the research of Steven Spear. The key point here is that before you can ask any of the following questions, you have to have a crisp and precise of what “good” looks like. In this paradigm, all processes are target conditions. And as the work is being done, we are actively searching for obstacles so we can work to make the work smoother and more consistent.
In other words, “What should be happening?” and “How do you know?”
Do the people doing the work understand the standard process as it should be done?
A few months ago I went into some depth on this here: Troubleshooting by Defining Standards. That probably isn’t the best title in retrospect, but there are too many links out there that I don’t want to break by changing it.
B. How do you know it is being done correctly?
Today I ask this question differently. I ask some version of “What is actually happening?” followed by “How can you tell?” We want to know if the people doing the work have a way to compare what they are actually doing against the standard.
C. How do you know the outcome is free of defects?
So, question B asks about consistency of the process, and question C asks about the outcome. Does the team member have a way to positively verify that the outcome is defect-free?
D. What do you do if you have a problem?
Again, we are checking if there is a defined process for escalating a problem. And we define “problem” as any deviation from the standard, or any ambiguity in what should be (or is) happening. We want someone to know, and act, on this, and the only way that is going to happen is to escalate the problem.
We want this process to be as rigorous and structured as the value-adding work.
And we want as much care put into designing production process as was put into designing the product itself. All too often great care and a lot of engineering time goes into product design, and only a casual pass is made at designing and testing the process.
Even better if these are done simultaneously where one informs the other.
For Abnormal Conditions:
ACT:
These are actions that the leader must take if she finds something that isn’t “as it should be” in the course of the CHECK questions above. Key Point: These are leadership actions. That doesn’t mean that the leaders personally carry them out, but the leaders are personally responsible for ensuring that these things are done – and checking again.
That is the only way I know of to prevent the process from continuing to erode.
A. Immediately follow up to restore the standard.
If it isn’t possible to get the intended standard into back place, then get a temporary countermeasure into place that ensures safety and quality.
B. Determine the cause of erosion.
We are talking about process erosion here, with the assumption that something knocked the process off its designed standard. Some obstacle has been discovered, we have to better understand what it is – at least enough to get it documented.
C. Develop and apply countermeasure.
Here we may have to run experiments against this newly discovered obstacle and figure out how to make the process more robust.
That is the end of the little card. But I want to point out that we didn’t just hand these out. You got one of these cards after time paired with a coach on the shop floor practicing answering and asking these questions. Only after you demonstrated the skill did you get the card – just as a reminder, not as a detailed reference. This exercise was inspired by a few of us who had experiences “in the chalk circle” especially with Japanese senseis who had been direct reports to Taiichi Ohno.
We piloted and developed this process on a very patient and willing senior executive – but that is another story for another day. (Thank you once again, Charlie. I learned more from you than you will probably ever realize.)

































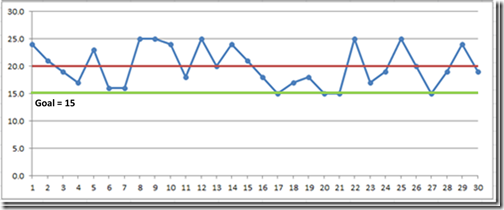
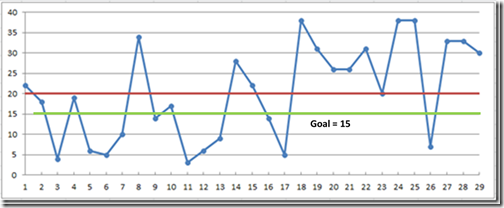
 Sometimes people fall into a trap of believing they understand a process if they can successfully predict it’s outcome. We see this in meetings. A problem or performance gap will be discussed, and an action item will be assigned to implement a solution.
Sometimes people fall into a trap of believing they understand a process if they can successfully predict it’s outcome. We see this in meetings. A problem or performance gap will be discussed, and an action item will be assigned to implement a solution.